Validation of COMBINE for virtual screening
Introduction, comments, relevant literature notes etc
I see the whole project in the context of targeted / knowledgebased scoring vs physics bases (eg MMPBSA, LIE, PBbinding calcs). Both approaches start to get within computational reach for virtual screening and library design and hence it is useful to establish what one can expect. COMBINE is, at least to me, on the extreme when it comes to knowledge based scoring functions if one stays within one series it is well established that the results are excellent. For libdesign the challenge is to select binders from a set of molecules with a identical scaffold (geometry) challenge for most docking programs, hence the value of more detailed scoring functions.
uPA data
Some notes on the dataset
make a table with molecule picture, pIC50, reference, and pdbcode for supplementary material. a short write up including that we are aware of the problem mixing ligands from several labs
development and validation of a COMBINE model
technical procedure , variable selection procedure and final plots (q2, expt vs predicted, residuals)
Use of COMBINE models to score docking solutions
Write up methods for docking (how was receptor prepared etc)
In this section we look at the feasability of using COMBINE to score docked structures in a virtual screening setting. The experiment proceeds in three stages:
Using the training set with known Xray structures to look at how well does docking docking + minimisation reproduce xrays (ie rmsd plots, simply histogram of rmsds + one picture of a successful docking). Having established a docking protocol we move on to look at binding affinity prediction for the training set. (section training set below) we also need to score the final poses with ZAP for reference since we will compare with this later.
Looking at a test set of known Kis (but unknown Xray structure), use GOLD to predict binding mode and then score with COMBINE or ZAP for binding affinity prediction.
Looking at random molecules (with an extremely low probability of binding) to see how they score with the model here we use the NCI datasset. This is to emulate a virtual screening setting the obvious critisism is that it is trivial to computationally separate NCI from proteases maybe we can do a matched set of inhibitors as well
Training set
Redocking of inhibitors used to develop COMBINE model (GOLD)
details on the method and receptor used
Results:
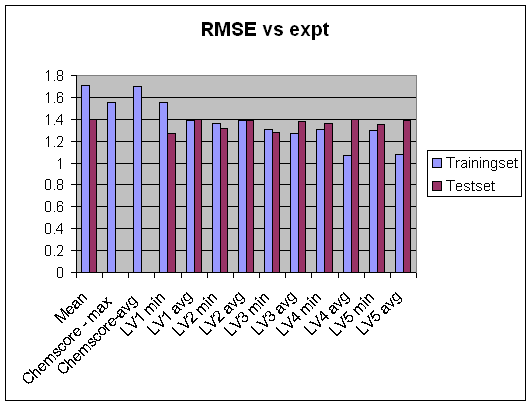
Look at the binding energy prediction for the training dataset. There are a set of baseline models that we compare with. The most simple model is Ki = Ki (ie we set the prediction to the mean for training set) and look at the error in predictions. We also compare with using Gold Chemscore and ZAP.
It looks as if the LV4
LV5 scores
performs best for training set make a plot of Rsquare RMS error
to
prove/illustrate this
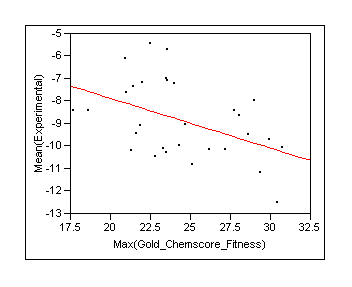
|
|
|
||
|
RSquare |
0.207084 |
||
|
RSquare Adj |
0.178765 |
||
|
Root Mean Square Error |
1.546532 |
||
|
Mean of Response |
-8.86933 |
||
|
Observations (or Sum Wgts) |
30 |
||
|
|
|
||
|
Mean |
-8.86933 |
||
|
Std Dev [RMSE] |
1.706574 |
||
|
Std Error |
0.311576 |
||
|
SSE |
84.45949 |
||
Compare selection methods
- Using the top pose from virtual screening (GOLD chemscore), subject this to amber minimisation + COMBINE (this would be the most efficient protocol in terms of computational cost)
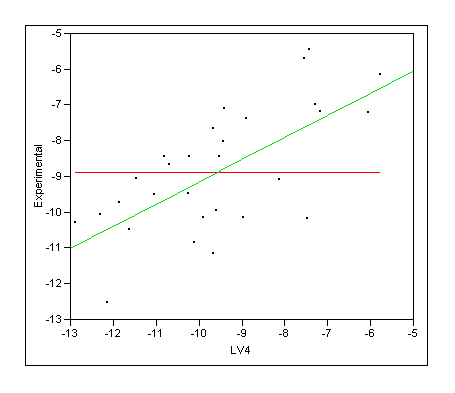
|
LV4 |
|
|
RSquare |
0.450632 |
|
RSquare Adj |
0.431012 |
|
Root Mean Square Error |
1.287291 |
|
Mean of Response |
-8.86933 |
|
Observations (or Sum Wgts) |
30 |
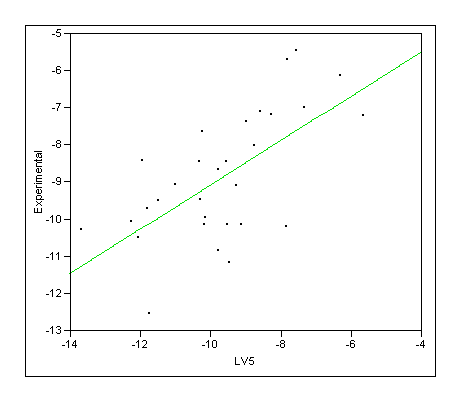
|
|
|
|
RSquare |
0.417038 |
|
RSquare Adj |
0.396218 |
|
Root Mean Square Error |
1.326067 |
|
Mean of Response |
-8.86933 |
|
Observations (or Sum Wgts) |
30 |
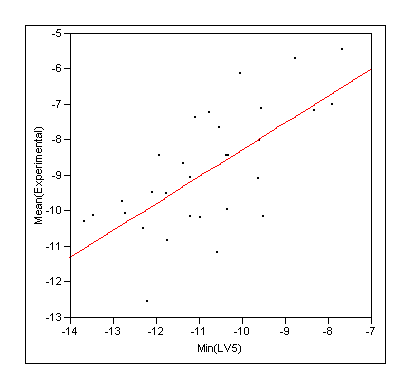
- Rescore the docking ensemble with COMBINE and take the lowest energy (ie predicted tightest binding) molecule as the solution (ie re-rank with COMBINE)
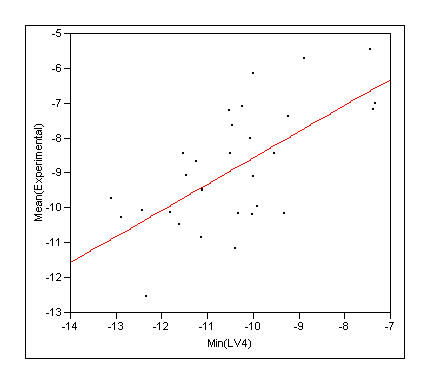
|
RSquare |
0.423632 |
|
RSquare Adj |
0.403048 |
|
Root Mean Square Error |
1.318545 |
|
Mean of Response |
-8.86933 |
|
Observations (or Sum Wgts) |
30 |
|
RSquare |
0.465337 |
|
RSquare Adj |
0.446242 |
|
Root Mean Square Error |
1.269946 |
|
Mean of Response |
-8.86933 |
|
Observations (or Sum Wgts) |
30 |
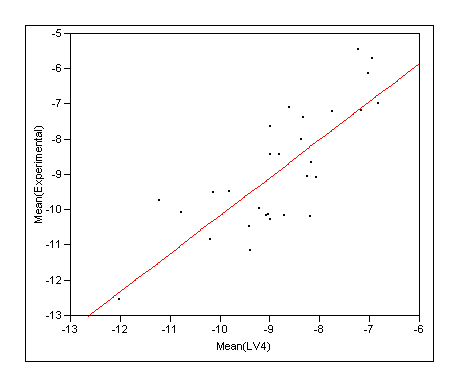
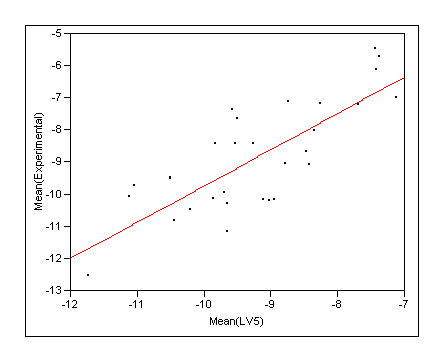
- Rescore the docking ensemble and take the ensemble average from COMBINE seems to give most robust predictions
|
RSquare |
0.618364 |
|
RSquare Adj |
0.604734 |
|
Root Mean Square Error |
1.072927 |
|
Mean of Response |
-8.86933 |
|
Observations (or Sum Wgts) |
30 |
|
RSquare |
0.614585 |
|
RSquare Adj |
0.600821 |
|
Root Mean Square Error |
1.078225 |
|
Mean of Response |
-8.86933 |
|
Observations (or Sum Wgts) |
30 |
Test set (Celera/Axys)
details on dataset
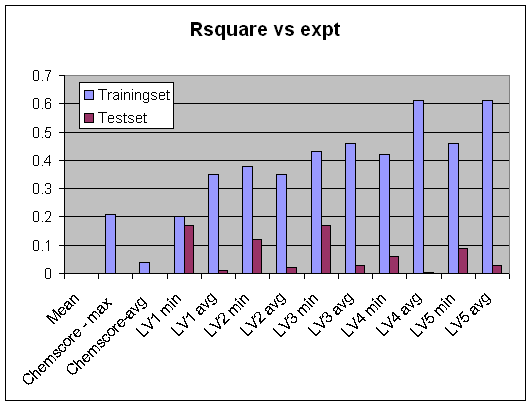
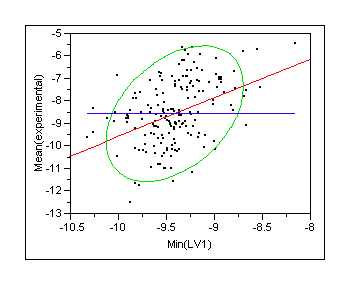
Here there is a rapid decrease of performance with number of latent variables little predictive value beyond the first one so to some degree the model is overfitted (or argualby not fit for purpose...) again illustrate with plots of Rsquare vs number of latent variables for the different selection methods.
|
|
|
|
RSquare |
0.167599 |
|
RSquare Adj |
0.162923 |
|
Root Mean Square Error |
1.287089 |
|
Mean of Response |
-8.54581 |
|
Observations (or Sum Wgts) |
180 |
for this dataset we also
want to look at
the chemscore performance and ZAP preformance.
The correlation with experimental Ki values is atrocious but that is usually the case for scoring functions they might still be useful for virtual screening next section
NCI dataset
Here we want to look at enrichments for the different selection methods this is a standard virtual screening exercise but arguably a rather easy case (not much value in this)
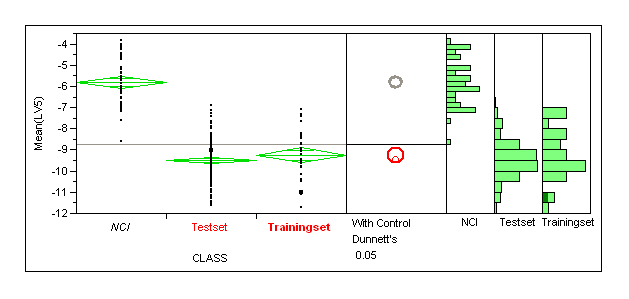
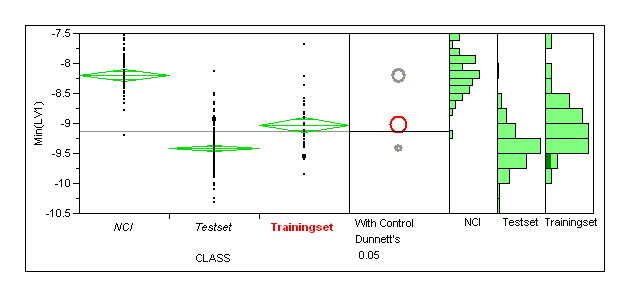
Need to produce enrichment plots for the dataset. Would be good to run this for a larger set of NCI compounds (and also a matched property set I guess we could use our old thrombin dummies)
Performance on library set score within one scaffold. Look at overall performance and performance per library